|
Bells were originally just rung in order from the smallest
(highest note, usually called the treble)
to the biggest (lowest note, usually called the tenor), this is called rounds and is
written out on a line, like this:
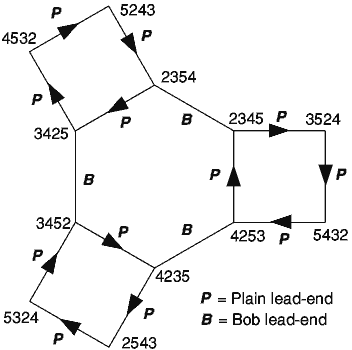
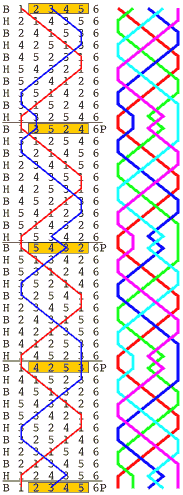
1 2 3 4 5 6 This sounds boring after a while, so about 400 years ago, change ringing was invented. Ways of changing the order were found and written down, with the next order on the next line, as in the column on the far left, which represents a method called 'A Plain Course of Bob Doubles'. The leftmost column, is only 'B' or 'H', to show which row is handstroke and which a backstroke. The path of the treble is shown by a red line, that of bell 3 by a blue one. In this method there are 10 rows between where the treble starts in the first place and where it gets back to the first place, these 10 rows are called a lead. A black line is drawn under the line where this happens to make it easier to see, and a letter 'P' written at the end of the next line to show this is a Plain lead. The method continues in a predefined way until the bells return to rounds at the bottom, after 4 leads or 40 rows. Since there are 5 changing bells if we want to ring the bells in all possible combinations of the 5 numbers, we must ring 120 rows (factorial 5, 5*4*3*2*1), making 12 lead-ends. The other changes and lead-ends are visited by changing the type of lead-end; the conductor calls "Bob" two rows before the treble gets back to the first place. This tells the ringers to change their order and then continue as before; when this happens a 'B' is printed at the lead end. 120 lines take much more space to write out than 40, so to make a more compact diagram leave out the lines where the bells are just 'plain hunting', look at the column on the right showing just the path of the bells, with each bell its own colour. The pattern only changes at the lead ends, so we can print just those rows, leaving the ringers to plain hunt in between. |