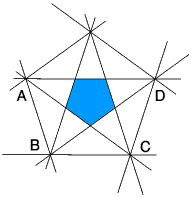
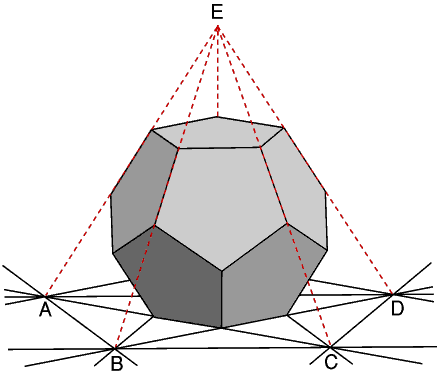
Stand the dodecahedron on
one face and imagine projecting the other faces down on to the plane of that
face. Each will meet it in a line. The lines will join at the points such as
A, B, C, D.The diagram in the plane is called the stellation diagram.
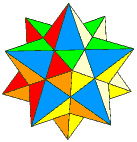
If you project the faces from the plane they meet at E, forming a pentagonal pyramid standing on the face. In this is a way you can form a new polyhedron from the original one.
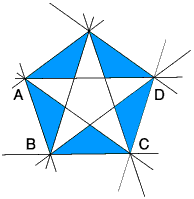
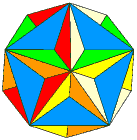
Alternatively you can select areas of the stellation diagram to form the faces of a new polyhedron.
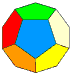
The diagrams below show which areas to select to make the polyhedra shown in the row beneath them.
