A posy of 'tulips'

Make yourself a posy of polyhedral tulips

To make this model you will need:

Wakefield tulips

Download the zipped Drawfiles (download size 31K) or as PDF download size 36K. Then follow the directions below to make the model on the left.
The Draw files (PDF pages) needed to make a copy of the 'Tulips' on show on the Fortran Friends stand at Wakefield 2001 are in this zipped directory (PDF file).

Draw
file		 PDF
page		 colour parts provided
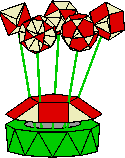
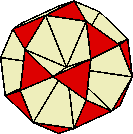
Base+A1 2 cream the petals of the Tetrahemihexahedron (A) plus the cream triangles of the pentagonal cupola base
Base+A2 3 red the outer triangles of the Tetrahemihexahedron (A) plus the red parts of the pentagonal cupola base
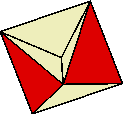
PetalsB+C 4 cream the petals of the Octahemioctahedron (B) and the Cubohemioctahedron (C) (you need two of these)
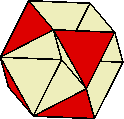
PetalsD+E 5 cream the petals of the Small icosihemidodecahedron (D) and the Small dodecahemidodecahedron (E) (you need two of these)
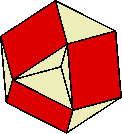
OuterBCDE 6 red the outer parts of the models:
B (8 large triangles)
C (6 squares)
D (20 small triangles)
E (12 pentagons)
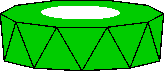
StandB 7 green the bottom of the stand (half a decagonal antiprism) with half the sides
StandT 8 green the top of the stand with the other half of the sides (half a decagonal antiprism with a big hole in it)

Instructions

The Draw file 'TulipPlan' (page 1 of the PDF) shows the final object and the three 'flower' types without their outer parts so that you can see how they fit together. Print this out so you can follow it easily while you make up the models.
Print the sheets to be cut out on the thickest coloured paper which your printer will allow. We used 160 gm paper for the models on show at Wakefield.

The Tetrahemihexahedron

model A

Wakefield tulip A

Start with the simplest model A.
To construct this model (and the pentagonal cupola base) you will need to print the files 'Base+A1' (we used cream paper for this) and 'Base+A2' (red) [pages 2 and 3].
Carefully cut round the 7 pieces at the top of 'Base+A1' which are going to make the petals of this model. Note that each piece has tabs on all its sides.
Score only along the lines which make the tabs; the internal lines are only for reference and should NOT be scored.
Fold the tabs all the same way on the 4 simple triangular pieces. (We find that if you fold them towards the inked line, the ink makes less mess of the final model.)
On the two pieces with two triangles, fold the two tabs on one triangle up and the two on the other triangle down.
On the last piece with 4 triangles fold the tabs up and down alternately.
Follow the diagram to glue one of the pieces with two triangles to the one with four. Make sure that the two tabs on each half of the 2-triangle piece face the same way as the tabs on the 4-triangle piece. The tabs which are going to join these petals to the triangular outer parts are shown transparent only for the top left part of this diagram. The others have been omitted for clarity.
Next glue in one of the single triangle pieces to support the 2-triangle piece as shown for the top-left octant of this model. The three external tabs should all be facing the same way so that the outer red triangle can be glued straight onto them.
Turn the model round and glue on another 1-triangle piece in exactly the same way.
Turn the model over. This face of the 4-triangle piece has not got lines on it to guide you but glue the other 2-triangle piece and the two 1-triangle pieces on it in the same way using the petals on the other side to show you their positions.
Finally glue on the four red outer triangles from 'Base+A2'.
Put aside the rest of the sheets 'Base+A1' and 'Base+A2' for later.

The Octahemioctahedron and the Hexahemioctahedron

model B model C
Look at the final models marked B and C in the picture of the bunch. You should see that the structures of the cream petals are the same; the only difference between them is that eight red triangles are stuck on one of them and six squares are stuck on the other. This is why there is only one diagram showing how to construct the cream petals (centre right).
For B the internal and external tabs must all be inside the triangular parts (to be covered up by the red outer triangle faces), leaving the open square faces without any visible tabs. The opposite happens for the model C.
Cut out the pieces from a cream sheet 'PetalsB+C' [page 4] and score only along the tabs.
Fold the tabs on the 6-triangle piece in alternate directions. On the 3-triangle pieces fold the tab on the central triangle the opposite way to the other four. On the 2-triangle pieces fold the tabs on one triangle one way and the tabs on the other the other way. The tabs on the single triangles should all be folded the same way.
The principle of gluing these models is the same as for model A but you must always be thinking of which way the tabs are supposed to go.
Glue the 3-triangle piece to the 6-triangle piece and support it with two single triangles as shown on the upper right of the diagram.
Glue a 2-triangle piece between the 3- and 6- pieces and support this each way with 1-triangle pieces as shown on the top back of the diagram.
Turn it over and do the same again on the other side of the 6-triangle piece.
Finally glue on the 8 large red triangles (or 6 squares) from 'OuterBCDE' [page 6].

The Small icosihemidodecahedron and the Small dodecahemidodecahedron

model D model E
Model D (with 20 external triangles) and model E (with 12 external pentagons) are a similar pair of models. The cream petals are the same for both except that the tabs face the opposite ways.
Cut out the pieces from a cream sheet 'PetalsD+E' [page 5] and score only along the tabs.
Fold the tabs on the 10-triangle piece in alternate directions.
Fold the tabs on all short edges the other multiple-triangle pieces in alternate directions and the ones on the two long edges in the same direction as the tabs on the short edges of their triangles.
The tabs on the single triangles should all be folded the same way.
The gluing works the same way as for the previous pair of models. Glue the 5- to the 10- and support it with two single triangles, ensuring that the tabs point the right way. This is shown in the diagram at the bottom of the page with the 10- horizontal and the 5- above it and going off to the left.
Next glue a 4- to the other side of the 5-, again ensuring that the tabs go the right way (if the 4- pieces have tabs pointing the wrong way, don't fold them back but reflect its position; there are two ways the 4- piece will fit between the 5- and the 10- and only one will have the right tabs). Fill up the remaining spaces with 2- pieces and then 1- pieces (shown in the figure on the top left between the 5- and the 10-).
Turn the model over and do the same again on the other side of the 10-triangle piece.
Finally glue on the 20 red triangles (or 12 pentagons) from 'OuterBCDE' [page 6].
This completes the flowers.

Now make the base which comes in two parts: Cut out all the parts and score along the internal lines for folding.
Obtain 5 plastic drinking straws for the stalks and punch out the holes (marked as solid black circles) in the pentagonal cupola.
Fold them up and glue the two models. You can stick the two parts together to form the base when you are sure that the straws go through the holes nicely.
It then becomes a gyroelongated pentagonal cupola which is one of the Johnson solids.

This finishes the base.
Push a small piece of blu-tac into the middle of one opening on each flower and gently push a straw into it. Then arrange your flowers in their stand.

Well done! Now it's time for tea.
Click here to download a demo version of the !PolyNet program used to make these files (size 130K).
Click here to see more models to make

Page last updated 28 January 2014
Click here to return to 'Fortran friends' top page