Space filling
We can think of building up a crystal from a set of identical building
blocks or polyhedra. The shape of these blocks is fixed by the atoms
from which they are made. Some are cubic
like this one, with an atom at each corner of the cube.
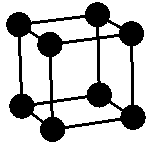
Cubes have square sides. If some of the sides are rectangles they can
still pack together to fill space. Do you think that all space filling
blocks have sides which meet at right angles?
Some insects build space filling blocks in their nests; for example
bees store honey
in hexagonal honeycombs. They look like the left hand diagram below:
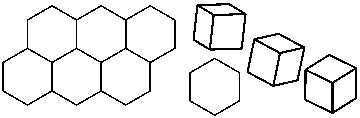The right hand diagram shows a view of a cube rotated until it has a
hexagonal outline like the honeycomb shapes. Do you think that honeycombs
are made from cubes but we do not realise this because we do not look at
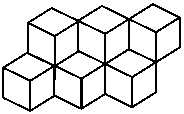
them from the correct direction.? Here is a set of cubes filling space
which look similar to the honeycomb.
There may be other shapes which can fill space. If you were a bee you
would want to enclose the biggest volume you could make from the smallest
area of beeswax. What about this shape?
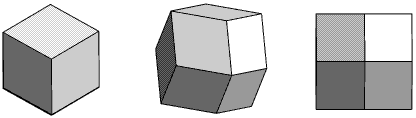The sides have 4 corners, but unlike a cube which always has just 3 sides
meeting at each corner, this shape has some corners with 4 sides meeting.
The diagram below shows the 3 sides meeting at a corner on the left,
the middle diagram shows it after a small rotation, and on the
right the rotation continues until you can only see the 4 sides meeting at
a corner, when the outline has become square.
So this shape sometimes looks similar to
a cube which has a square outline when seen from some directions.
This shape is called a rhombic dodecahedron.
The name comes from the ancient Greeks;
dodec meant 12, hedron meant a solid shape, so
dodecahedron is a solid with 12 faces, rhombic describes
the shape of each face, they have 4 sides but they are not squares.
More spacefilling polyhedra can be seen on
another page
Click here for instructions on how to make
your own models and try fitting
them together to see how well they fill space.
Page last updated 7 September 2003
Click here to return to 'Fortran friends' top page